Un singolo tassello che garantisce una tassellazione aperiodica: an aperiodic monotile
Il 20 marzo 2023 è uscito un preprint ( https://arxiv.org/abs/2303.10798 ) dei matematici David Smith, Joseph Samuel Myers, Craig S. Kaplan e Chaim Goodman-Strauss dal titolo
An aperiodic monotile, con la dimostrazione di una tassellazione aperiodica formata da copie di un singolo tassello con 13 lati (vedi anche il link sul sito MAddmaths)
Questo risultato migliora quello del 1974 di Roger Penrose, con la famosa tassellazione aperiodica ottenuta con copie di due quadrilateri (l’aquilone e la freccia). In realtà il nuovo tassello (chiamato il cappello, dai quattro autori) va necessariamente usato da entrambe le facce: cioè si potrebbe dire che i tasselli sono ancora due ma uno è il ribaltamento dell’altro.
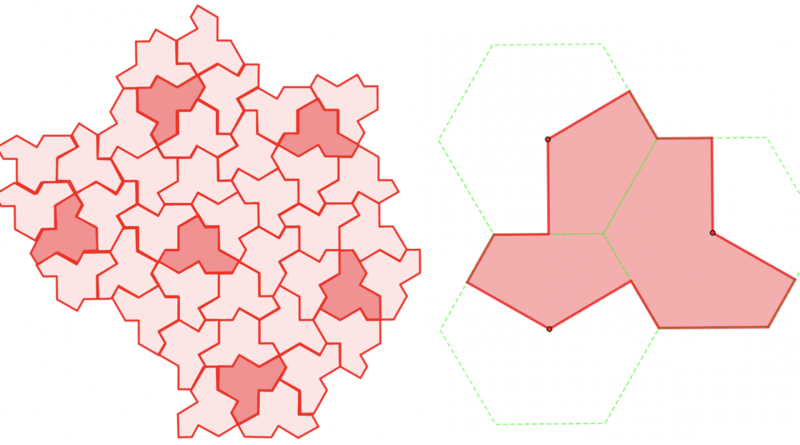
In figura: a sinistra un esempio di tassellazione: i tasselli rossi sono ribaltati rispetto a quelli rosa. A destra: la costruzione del cappello partendo da tre esagoni regolari come in figura. Le immagini sono di Corrado Falcolini, prodotte con Geogebra.